SEMINAR 2025
Algebraic Topology Principles behind Topological Quantum Error Correction
| Speaker | Xiang Zou, University of Toronto, Canada |
| Date/Time | Tuesday, 2 Sep, 3pm |
| Location | S11-02-07 Conference Room |
| Host | Prof Lo Hoi Kwong |
Abstract
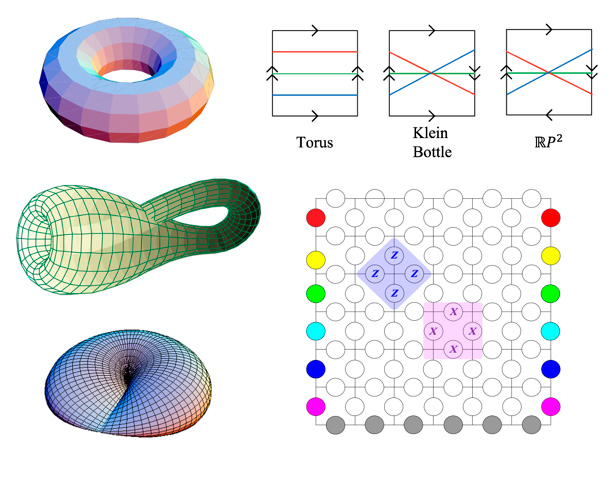
Quantum error correction (QEC) is crucial for numerous quantum applications, including fault-tolerant quantum computation, which is of great scientific and industrial interest. Among various QEC paradigms, topological quantum error correction (TQEC) has attained the most experimental successes by far. In this paper, we build upon existing knowledge of TQEC by developing a generalized theoretical framework of TQEC. We begin by formally defining TQEC codes and exploring the algebraic topological principles underlying these quantum codes, including deriving the conditions for any topological manifold to serve as a quantum memory. We show that TQEC for qubits works for both orientable and non-orientable manifolds. Moreover, we extend the construction of TQEC to higher-dimensional manifolds and provide examples for higher-dimensional TQEC codes. Finally, we apply these principles to construct new codes on 2-dimensional manifolds that have received limited attention in prior literature. As a case study, we simulate the performance of TQEC codes on the Klein bottle and RP2 and evaluate their efficacy for quantum error correction.

Biography
Xiang Zou is a third-year Ph.D. candidate in the Department of Physics at the University of Toronto, working under the supervision of Professor Hoi-Kwong Lo. He obtained his undergraduate degree from the University of Hong Kong, with a major in Physics and minored in Computer Science. His research focuses on quantum computation, with particular interests in quantum error correction, photonic cluster-state generation, quantum channel simplification, and quantum machine learning.
