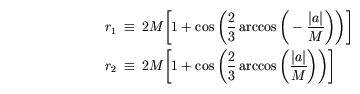
where a is the angular momentum per unit mass of the black hole. Note that in the limit of zero rotation, these two orbits coincide at r = 3M, giving the single circular orbit of the Schwarzschild black hole.

In the case of a rotating Kerr black hole, there are two circular photon
orbits that could exist in the equatorial plane. One is a prograde
orbit moving in the same direction as the black hole's rotation, while
the other is a retrograde orbit moving against the black hole's rotation.
Their radii are respectively given by
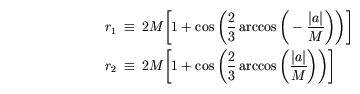
where a is the angular momentum per unit mass of the black hole.
Note that in the limit of zero rotation, these two orbits coincide at
r = 3M, giving the single circular orbit of the
Schwarzschild black hole.
It is perhaps less commonly known that spherical orbits - i.e., orbits with constant radii that are not confined to the equatorial plane - of photons are also possible around a Kerr black hole. Such orbits were first studied in the timelike case by Wilkins [2] some years ago. Here, I shall consider the possibility of spherical photon orbits which generalise the two above-mentioned circular orbits. Their properties are briefly discussed, and `wire-frame' models of selected orbits are produced with the aid of a Java applet. I hope that you will be amazed as I have with the possible patterns that these orbits can trace out in three-dimensional space.
It was shown in Ref. [3] that for orbits with constant
radius r, the relevant geodesic equation can be solved to give
a one-parameter class of solutions parameterised in terms of
r:
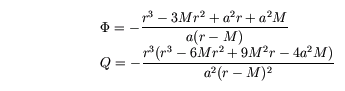
where Phi and Q are constants of motion proportional
to the photon's angular momentum and Carter's constant, respectively.
These solutions are physical only if Q is positive
[3], which restricts r to the range
r1 < r < r2.
At either end of this range, Q vanishes, giving the
two equatorial orbits mentioned above. As with those orbits, these
solutions are unstable under radial perturbations.
The following graph shows the general behaviour of Phi and Q
as a function of r:
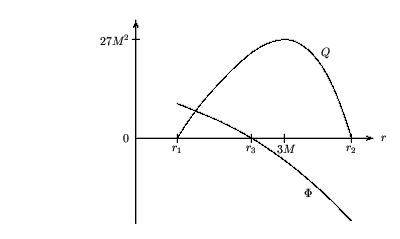
As can be seen, Q monotonically increases from zero at
r = r1, to a maximum value of
27M2 at r = 3M, before
monotonically decreasing back to zero at
r = r2. On the other hand, Phi
monotonically decreases from some positive value at
r = r1, to some negative value at
r = r2. It vanishes at the intermediate radius:
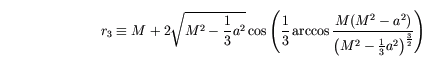
Orbits with positive Phi are prograde, while those with
negative Phi are retrograde.
Other properties of these spherical photon orbits can be deduced from the geodesic equations. For example, it is possible to show that the maximum latitude that the photons can reach depends inversely on |Phi|. In particular, they can reach the north and south poles if and only if Phi vanishes. It is also possible to obtain an analytic expression for the change in the photons' azimuth for one complete latitudinal oscillation of the orbit. For details of these and other properties, the reader is referred to Ref. [3].
In each of the following examples, the orbits are plotted on an imaginary sphere of fixed radius. Each orbit begins at the equator and heads southwards. The observer is assumed to be located 30° west of the starting point of the orbit, and 60° north of the equator. The sense of rotation of the black hole itself is from west to east from the viewpoint of the observer.
For simplicity, we shall consider only the case of an extreme Kerr black hole, i.e., when a = M. (Orbits for a < M turn out to be qualitatively similar; see the complete table of examples below). In this case, Phi takes the physically allowed range -7M < Phi < 2M.
We begin with the special case Phi = 0 (corresponding to
r = r3), which describes a photon with
zero angular momentum. Despite this, such a photon can still orbit
the black hole at constant radius due to the dragging of inertial
frames around it, as predicted by the well-known
Lense-Thirring effect.
Furthermore, since Phi vanishes, the photon's orbit
will take it through all possible latitudes, right to the north and
south poles. The figure below shows two latitudinal oscillations of
this orbit:
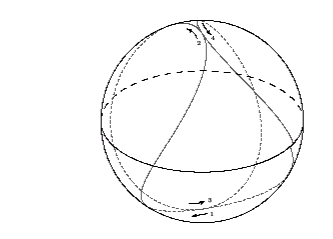
For clarity, numbered arrows indicate the order and direction of motion.
Clicking on the figure gives a three-dimensional wire-frame model of
this orbit which can be examined from any angle (try it!).
Our next example, Phi = -2M (r = 3M),
is also special in the sense that it is the unique orbit which has the
maximum allowed value of Q, namely 27M2.
This implies that the photon is moving vertically whenever it is at
the equator [3], a fact that is clear from the
following plot showing three latitudinal oscillations of this
orbit:
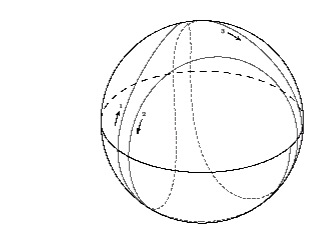
On the whole, however, it is a retrograde orbit with negative
angular momentum. This behavior can be understood from the Lense-Thirring
effect: the dragging of inertial frames is strongest at the equator, and in
this case, it precisely cancels out the retrograde motion of the photon.
Away from the equator, the dragging becomes weaker and so the orbit
regains its retrograde character.
When -2M < Phi < 0 (r3 < r < 3M),
it turns out that the photon orbits do not have a fixed
azimuthal direction. Five latitudinal oscillations for the case
Phi = -M is shown in the following figure:
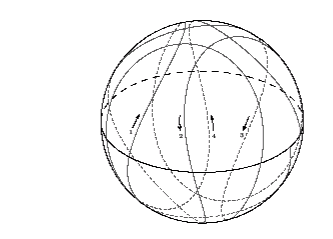
Observe that although the orbit is retrograde on the whole, it is
actually moving in the prograde-direction within a certain latitude of the
equator. This can again be attributed to the strength of the
Lense-Thirring effect in the equatorial region: in this case, the
negative angular momentum of the photon is not large enough to negate
this effect, resulting in it being dragged along in the direction of
the black hole's rotation.
For angular momentum -7M < Phi < -2M
(3M < r < r2), the orbits are
completely retrograde even in the equatorial region. This is because the
angular momentum of the photon is now large enough to dominate over the
Lense-Thirring effect. Four latitudinal oscillations for the case
Phi = -6M is shown in the following figure:
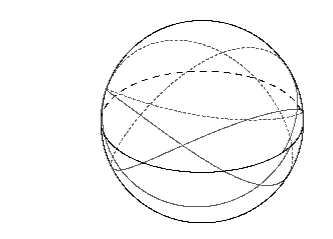
Another point to note from this figure, is the relatively low maximum
latitude of the photon. It goes to zero as Phi approaches
-7M, resulting in a retrograde circular orbit in the
equatorial plane.
We now briefly turn to the case when Phi is positive: 0 <
Phi < 2M (r1 < r <
r3), corresponding to prograde orbits. As an example,
one latitudinal oscillation of the orbit with Phi = M
is illustrated below:
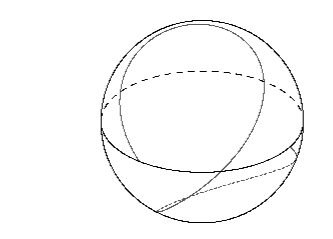
As can be seen, the photon swings right around both the south and north
poles, taking more than one revolution around the black hole to complete
one oscillation in latitude. A more extreme example is the case of
Phi = 1.999M:
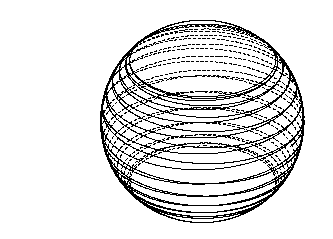
in which a helical pattern is apparent. The angle of inclination
of the photon is now so small that it takes more than 25 revolutions
to complete the one oscillation in latitude.
Finally, it should be pointed out that some rather interesting quasi-periodic patterns would result if the above photon orbits are continued for many latitudinal oscillations. These and other examples can be found by following the link below. Enjoy!
[2] D. C. Wilkins (1972) ``Bound geodesics in the Kerr metric,'' Physical Review D 5, 814-822.
[3] E. Teo (2003) ``Spherical photon orbits around a Kerr black hole,'' General Relativity and Gravitation 35, 1909-1926. [ps,pdf]